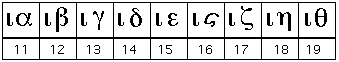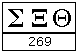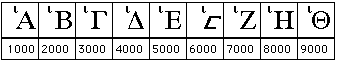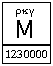انهيار الیقين *
هل يمكن میكنة الحقائق؟
محمد عامر
مقدمة :
يرى بعض المشتغلين بالعلوم الإنسانية أو فلسفتها أن
على هذه العلوم أن تنسج على منوال العلوم الطبيعية ، أو
ما يسمى بالعلوم المنضبطة . وهم يربطون هذا بقضية
استخدام الرياضيات كأداة ، كما يربطونه بقضية
اليقين .
ولما كان من المتعارف عليه أن الرياضيات هي قلعة
اليقين ، فقد يكون من المفيد أن يتعرف المشتغلون
بالعلوم الإنسانية على ما آلت إليه قضية اليقين في
الرياضيات ، حتى يقرروا لأنفسهم ما إذا كان من
المجدي أن يجعلوا ( أو يستمروا في جعل ) بلوغ اليقين
أحد أهدافهم .
وهذا المقال يركز على عرض وشرح النتائج التي
نشرها
كورت جودل Kurt Godel عام ۱۹۳۱ والتي تبين
- فيما تبين - أنه لا يمكن ( ولن يمكن ) الاطمئنان إلى خلو
كثير من النظريات الأساسية في الرياضيات من
التناقضات المنطقية . ويربط المقال بين هذه النتائج
وقضايا ميكنة الحقائق ، ثم يقدم ويناقش بعض الأفكار
الفلسفية المتعلقة بهذه الأمور .
نظرة تاريخية :
مرت الرياضيات في تاريخها بأزمات استوجبت إعادة
النظر في الأسس التي تقوم عليها ، ولعل أولى هذه
منذ حوالي أربعة وعشرين قرناً .
كان الفيثاغوريون يأخذون بـ « المسلمة » التالية ،
ويقيمون براهين هندستهم عليها . لكل قطعتين
مستقيمتين أ ب ، حـ د توجد قطعة مستقيمة هـ و
بحيث تكون كل من أ ب ، حـ د من مضاعفات هـ و. أي أننا إذا أخذنا هـ و كوحدة لقياس الطول ، كان كل من
طول أ ب وطول حـ د عدداً صحیحاً . وكانت هذه « المسلمة » متفقة مع عقيدة الفيثاغوريين الكونية التي تجعل الأعداد
الصحيحة أساس كل شيء . لكنهم - لبالغ أسفهم - اكتشفوا أن هذه « المسلمة » غير صحيحة . فقد استطاعوا إثبات
أنه إذا كان ح ط ي ك مربعا وكانت القطعة أ ب هي الضلع ح ط ، والقطعة حـ د هي القطر ح ي ، لما وجدت قطعة
هـ و تحقق الشروط المطلوبة . فزعزع هذا عقيدتهم كلها وليس هندستهم فقط .
وقد ظلت الهندسة في أزمة إلى أن وضع
يودوکسس ( ٤۰۸ - ۳٥٥ ق. م ) تعريفه للتناسب . فدخلت بذلك
الهندسة عصراَ جديداً ، هو العصر الذي تسمى هندسته بالهندسة الأقليدية ، إذ أنها قد انتقلت إلينا من خلال كتاب
لنقفز الآن ۲۳۰۰ سنة من الزمان لنصل إلى الأزمة التي شهدتها الرياضيات مع دورة القرن التاسع عشر ، والتي
كانت نتائج جودل من تداعياتها . ولنوفر على القارىء مؤونة الدخول في تفصيلات فنية قد لا يستسيغها ، نكتفي
بالقول بأن هذه الأزمة بلغت من العنف حداً استوجب إعادة النظر ليس في الرياضيات ذاتها فقط ، بل أيضا في المنطق
الذي تقوم عليه الرياضيات ، وفي اللغة التي تصاغ من خلالها الرياضيات .
وكتمهيد لعرض نتائج جودل سنناقش فيما يلي بعض المشكلات المنطقية ، ومن خلالها سنتعرض لبعض القضايا
اللغوية . وسنحاول تجنب أو تبسيط الأمور الفنية قدر الإمكان . وعلى كل فنحن ندعو القارئ إلى عدم التهيب من هذه
الأمور الفنية ، كما ندعوه إلى عدم التهيب من التعامل مع الرموز القليلة التي سنضطر إلى استخدامها .
الصدق :
الصدق عكس الكذب ، وكل منهما صفة من صفات الجُمَلْ ، أو بالأحرى بعض الجمل ، فالجمل الإنشائية لا
توصف بالصدق ولا بالكذب . لكننا نود أن يكون بالإمكان وصف كل جملة خبرية ( ذات معنى ) بالصدق أو
بالكذب ، وليس بالاثنين معاً . هنا تقابلنا عقبة كأداء ، يمكن تجسيدها في الجملة التالية :
هذه الجملة كاذبة
فإذا ما افترضنا أن الجملة المكتوبة على السطر السابق صادقة خلصنا إلى أنها كاذبة ، والعكس بالعكس .
لأسباب كهذه اصطنع المناطقة لغات رمزية تبلغ من الضعف حداً لا يسمح بأن نصوغ فيها جملة تكذب نفسها .
وفي نفس الوقت تكون على قدر من القوة يكفي لأن نصوغ فيها نظریات رياضية ( أو علمية ، بصفة عامة ) هامة .
كيف نتعامل مع اللغات الرمزية من حيث الصدق والكذب ؟ لننظر في المثال التالي ، الذي سنصوغه صياغة
نصف رمزية تخفيفاً على القارىء .
لكل س ، توجد ص ، بحيث ( س = ص + ص )
هل الجملة السابقة صادقة ؟ الجواب يتوقف على الإطار الذي نفسرها فيه . فإذا كان الإطار هو الأعداد
الطبيعية : صفر ، ۱ ، ۲ ، ۳ ، . . . معرفاً عليها الجمع ، كان الجواب بالنفي لأننا لو أخذنا ۳ كقيمة س ، لما
وجدنا عدداً طبيعياً ص بحيث ( ۳ = ص + ص ) . أما إذا كان الإطار هو الأعداد الكسرية معرفاً عليها الجمع ، فإن الجواب
يكون بالإيجاب . لأنه إذا كانت س عدداً کسرياً ، فإن س/2 عدد کسري أيضاً . ولذا فما علينا إلا أن نأخذ س/2 كقيمة
ص لنجد ( س = س/2 + س/2 = ص + ص ) .
وعلى هذا فصدق الجملة أو كذبها لا يتوقف عليها وحدها ، وإنما يتوقف - بصفة عامة - على إطار التفسير أيضاً .
والجمل الصادقة في جميع الأطر تسمى جملا صادقة منطقيا ، وتلك الكاذبة في جميع الأطر تسمى جملا كاذبة منطقيا .
البرهان :
فكرة إقامة البراهين على مسلمات فكرة قديمة ، ترجع إلى عصر إقليدس ، على الأقل . أما الجديد فهو ألا ننتقل
من خطوة في البرهان إلى خطوة أخرى إلا على أساس قواعد محددة سلفاً تسمى قواعد الاستنتاج . هذه القواعد ليست
اختيارية تماماً ، بل يراعى في اختيارها أن تسمح بانسياب الصدق . أي أنه إذا كانت إحدى القواعد تنقلنا من عدة جمل
( تسمى المقدمات ) إلى جملة ( تسمى التالية ) ، فإن التالية تكون صادقة في كل إطار تصدق فيه جميع المقدمات . أيضاً
يراعى في اختيار قواعد الاستنتاج أن تكون واضحة ، بحيث يسهل تبين مواضع تطبيقها ، كما يسهل تطبيقها نفسه ،
بل إن كلا من هذا وذاك يجب أن يكون بالإمكان إجراؤه بطريقة ميكانيكية .
وكمثال على قاعدة استنتاج يسهل أن نرى أنها تتمتع بكل الصفات السابقة ، نذكر قاعدة الفصل وهي :
من ( أ ← ب ) ، أ ينتج ب
حيث كل من أ، ب جملة ، أما السهم « ← » فهو يعني الاستلزام . المقدمات هنا هي أ ، ( أ ← ب ) ، أما
التالية فهي ب .
بالاستعانة بقواعد الاستنتاج ، يمكن أن نعرف البرهان على أنه متابعة منتهية (١) من الجمل ، كل منها مسلمة ،
أو يمكن استنتاجها - من جمل سابقة عليها في المتابعة - بإحدى قواعد الاستنتاج . الجملة الأخيرة في المتابعة تسمی
مبرهنة ، والمتتابعة تسمى برهانها .
هل ثمة شروط على المسلمات ؟ بصفة عامة لا ، لكننا نود في كثير من الأحيان أن يكون من السهل التعرف
عليها ، بل أن يكون بالإمكان أن نتعرف عليها بطريقة ميكانيكية . أي نريد أن تكون هناك ماكينة ( كمبيوتر مثلا ) إذا
ما أعطيناها أية جملة من جمل لغتنا الرمزية قالت لنا - خلال فترة محدودة من الزمن - ما إذا كانت هذه الجملة مسلمة أم
لا . وواضح أن هذا الشرط يكون مستوفی دائماً إذا ما كان عدد المسلمات منتهيا . لأنه ما على الماكينة في هذه الحال إلا
أن تقارن الجملة المعطاة بالمسلمة الأولى ، فإن كانت هي ، وقفت مجيبة بالإيجاب وإن لم تكن هي ، انتقلت إلى المقارنة
بالمسلمة الثانية ، وهكذا . فإن لم تكن الجملة أيا من المسلمات ، توقفت الماكينة مجيبة بالنفي .
سنقول لمجموعة من المسلمات إنها فعالة إذا كان بالإمكان التعرف عليها ميكانيكا . وبناء على الفقرة السابقة
تكون كل مجموعة منتهية من المسلمات فعالة . هل توجد مجموعة من المسلمات لا نهائية وفعالة في ذات الوقت ؟ نعم ،
ببساطة خذ مجموعة المسلمات على أنها المجموعة المكونة من كل الجمل . لكن هل توجد مجموعة غير فعالة ؟ هذا ما
سنعود إليه فيها بعد .
واضح أنه إذا ما اخترنا مسلماتنا بحيث تكون جميعها صادقة منطقيا ، كانت مبرهناتنا جميعها صادقة منطقياً
كذلك ، ماذا عن العكس ؟ هل يمكن اختيار مسلمات وقواعد استنتاج بحيث تكون كل الجمل الصادقة منطقياَ
مبرهنات ؟ نعم ، ببساطة اعتبر كل جملة صادقة منطقياً مسلمة ، وفي هذه الحال يمكن حتى الاستغناء عن قواعد
الاستنتاج تماماً ، ويصير كل برهان مكوناً من جملة واحدة . لكن ماذا إذا ما اشترطنا في مسلماتنا أن تكون فعالة ؟
نالت هذه المشكلة قدراً كبيراً من اهتمام المناطقة . ويمكن القول بأنها قد حلت حلا إيجابياً بالنسبة للغات الرمزية
التي تعنينا هنا . أي أمكن التوصل إلى مسلمات فعالة ( سنسميها المسلمات المنطقية ) وقواعد استنتاج بحيث تكون كل
المبرهنات جملا صادقة منطقياً ، والعكس بالعكس .
النظريات :
بالاستعانة بالمفاهيم والتعريفات السابقه ، يمكن إزالة كثير من الغموض الذي يكتنف مفهوم « النظرية » . فكلما
ألحقنا بالمسلمات المنطقية مجموعة من المسلمات ( سنسميها مسلمات إضافية ) نتجت لنا مجموعة من المبرهنات التي
تختلف - بصفة عامة - باختلاف المسلمات الإضافية الملحقة . مجموعة المبرهنات هذه تسمى نظرية ، على وجه التحديد
النظرية المولدة بالمسلمات الإضافية .
قد يكون من المفيد أن نذكر على سبيل المثال ، نظرية الهندسة الاقليدية . من مبرهنات هذه النظرية الجملة
القائلة بأن مجموع زوايا المثلث مائة وثمانون درجة . نحتاج لبرهان هذه الجملة المسلمات الإضافية الخاصة بالهندسة
الاقليدية ، فهي لا يمكن برهنتها انطلاقاً من المسلمات المنطقية فقط . بل إننا إذا استبدلنا بمسلمات الهندسية الأقليدية
مسلمات إحدى الهندسات اللا إقليدية ، أمكننا البرهان على أن مجموع زوايا المثلث تختلف عن مائة وثمانين درجة .
بالرغم من أن الأساس المنطقي هو هو ، أي نفس المسلمات المنطقية ونفس قواعد الاستنتاج .
وحتى لا يحدث أي لبس ، نود أن نوضح أن أية جملة يمكن أن تختار كمسلمة إضافية . أي أننا لا نشترط في
المسلمات الاضافية أن تكون واضحة بذاتها أو أي شيء من هذا القبيل . فالمسلمات الإضافية هي إذن أقرب إلى
الفروض منها إلى المفهوم القديم للمسلمات .
هذا لا يعني أن المسلمات تختار اعتباطاً . فهناك عوامل علمية وتاريخية وجمالية وغير ذلك تؤثر في الاختيار .
وليس هنا مجال تفصيل هذا الأمر . ولذا فإننا سنكتفي بالحديث الموجز عن اعتبارين نحاول عادة أن نراعيها في اختيار
المسلمات الإضافية هما : الاتساق والفعالية .
يقال لنظرية ( أو لمجموعة المسلمات الإضافية التي تولدها ) انها متسقة إذا لم يكن من بين مبرهناتها جملتان
إحداهما تتنافى مع الأخرى . ويمكننا إدراك خطورة قضية الاتساق إذا ما عرفنا أن المناطقة قد أثبتوا ( الاثبات سهل ،
لكننا لن نثقل به على القارىء هنا ) أن النظرية غير المتسقة تشمل مبرهناتها جميع الجمل . أي أنه في حال عدم الاتساق
يمكن برهان كل جملة كما يمكن برهان نفي كل جملة ، وبذا تفقد النظرية جدواها .
الفعالية ، عرفناها من قبل . وأهمية أن تكون النظرية ذات مسلمات إضافية فعالة تكمن في أنه إن لم يكن الأمر
كذلك فسيتعذر التعرف على هذه المسلمات . بمعنى أننا إذا أعطينا جملة فقد لا نتمكن من الحكم على ما إذا كانت هذه
الجملة إحدى المسلمات الإضافية أم لا .
هناك أيضاً ميزة هامة أخرى . لنفرض أن لدينا مجموعة فعالة من المسلمات الإضافية . إذا أعطينا أية متتابعة
منتهية من الجمل فإنه سيكون بإمكاننا أن نعرف بالنسبة إلى كل جملة منها ما إذا كانت مسلمة ( منطقية أو إضافية ) ، أو
يمكن استنتاجها - من جمل سابقة عليها في المتتابعة . بإحدى قواعد الاستنتاج ، أو لا هذا ولا ذاك . ويمكن أن يجري كل
هذا بطريقة ميكانيكية .
وعلى هذا فبالنسبة إلى أية نظرية ذات مجموعة فعالة من المسلمات الإضافية ، تتحول عملية الحكم على ما إذا
كانت متتابعة منتهية ما من الجمل برهاناً أم لا إلى عملية ميكانيكية بسيطة ، بعد أن كانت عملية ذات أبعاد عقلية
ونفسية عميقة .
الاسئلة :
ما دام الاتساق وتوافر مسلمات إضافية فعالة ، من الصفات الهامة للنظريات ، فمن الطبيعي أن نسأل بالنسبة
إلى نظرية رياضية ما ، إذا ما كانت تتمتع بهاتين الصفتين .
وهذا ما فعله جودل بالنسبة إلى نظرية الأعداد . والمقصود بالأعداد هنا هي الأعداد الطبيعية : صفر ، ۱ ، ۲ ، ۳
، . . . . والذي أهل هذه النظرية لأن تكون موضع عناية جودل هو أنها نظرية محورية في الرياضيات وفي المعرفة
البشرية بصفة عامة ، وأن لها أهمية تاريخية فائقة ، وأنها بسيطة بالمقارنة بكثير غيرها من النظريات .
ما المقصود بالضبط بنظرية الأعداد ؟ اتخذ جودل لنفسه لغة رمزية ( لن نثقل على القارئ بتفصيلاتها ) يمكنه أن
يتحدث بها عن الأعداد وجمعها وضربها . وكما بينا في حديثنا عن الصدق ( انظر عاليه ) ، فإن صدق أو كذب جمل هذه
اللغة يتوقف على الاطار الذي نفسرها فيه ، والاطار الطبيعي للتفسير في حالنا هذه هو الأعداد الطبيعية معرفاً عليها
الجمع والضرب . سنسمي هذا الإطار ، الإطار الطبيعي .
مجموعة الجمل الصادقة في الإطار الطبيعي تكون نظرية ، سنرمز إليها بالرمز ݨ ، وهي ما سنعتبره - في هذا
المقال - نظرية الأعداد ، وأيضاً مجموعة الحقائق المتعلقة بالأعداد .
هل يمكن تولید ݨ من مجموعة من المسلمات الإضافية ؟ نعم ، ببساطة أجعل ݨ كلها مجموعة المسلمات
الإضافية . لكن ماذا عن الفعالية ؟ هل توجد مجموعة فعالة من المسلمات الإضافية بحيث تكون ݨ هي النظرية
المولدة بها ؟ هذا هو السؤال الأول الذي طرحه جودل(۲) .
لم يبدأ جودل محاولة الإجابة من فراغ . فقد كان لديه بالفعل
مسلمات نظرية الأعداد التي تنسب إلى الرياضي
الإيطالي
بيانو ( يقال أن الأصوب أن تنسب إلى الرياضي الألماني
دیدیكند ) . أعاد جودل صياغة هذه المسلمات في لغته
الرمزية ، وانطلق منها كمجموعة من المسلمات الاضافية . سنرمز إلى هذه المجموعة من المسلمات الإضافية بالرمز
ݥ ، وإلى النظرية المولدة بها بالرمز ࢶ .
يمكن بسهولة إثبات أن كل مسلمة في المجموعة ݥ صادقة في الإطار الطبيعي، وبالتالي فإن كل مبرهنة في ࢶ
صادقة بدورها في الإطار الطبيعي . وعلى هذا فالنظرية ࢶ هي جزء من النظرية ݨ .
يمكن بسهولة أيضا إثبات أن المجموعة ݥ فعالة . ومن ثم فإن النظرية ࢶ مولدة بمجموعة فعالة من
المسلمات . وعلى هذا فإذا كانت ( ݨ = ࢶ ) فإن الإجابة عن سؤال جودل الأول ستكون بالإيجاب .
هل ( ݨ =ࢶ )؟ هذا هو سؤال جودل الثاني . أما سؤال جودل الثالث فهو : ماذا عن اتساق ࢶ ؟
إذا كانت الاجابة عن السؤال الثاني بالإيجاب ، فإن قضية اتساق ݨ ستكون هي نفسها قضية اتساق ࢶ . أما
إذا كانت الإجابة بالنفي ، فإن اتساق ݨ يستلزم اتساق ࢶ والعكس قد لا يكون صحيحاً . أما لماذا اهتم جودل
باتساق ࢶ دون ݨ ، فهذا ما سيتضح فيما بعد .
الجمل والأعداد :
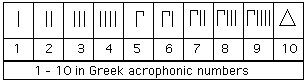
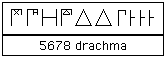
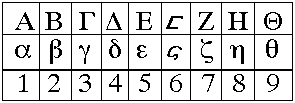
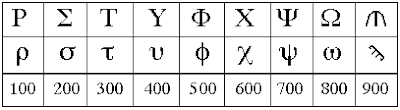
من قديم طوّر الناس ما يسمى بحساب الجمل . وهو - عند العرب المشارقة - عقد تناظر بين حروف الهجاء تبعاً
لترتيبها الوارد في أبجد هوز . . . وبين الأعداد . فالأحرف التسعة الأولى للآحاد ، والتي تليها للعشرات ، والتي تليها
للمئات ، والحرف الأخير « غ » ، للألف . وبذا تدل كل كلمة على عدد ، هو مجموع الأعداد التي تناظر حروفها .
وتدل كل جملة على عدد ، هو مجموع الأعداد التي تدل عليها كلماتها . فمثلا « في المشمش » تدل على ۸۰۱ . ولذا
فعندما سئل أحد الظرفاء عن تاريخ موت السلطان برقوق ، أجاب : في المشمش ( انظر المعجم الكبير - حرف الهمزة -
إصدار مجمع اللغة العربية عام ۱۹۷۰ - ص ۲۳ ) .
ويبدو أن جودل قد استفاد من هذه الأفكار ، فناظر بين رموز لغته وبين بعض الأعداد ، بطريقة ليس هنا مجال
شرح تفصيلاتها . سمحت هذه الطريقة لجودل أن يناظر أيضاً بين الجمل وبين بعض الأعداد ، وأيضا بين المتتابعات
المنتهية من الجمل وبين بعض الأعداد . لكن تركيز جودل لم يكن على أن الجمل تدل على أعداد ، بل على أن بعض
الأعداد تدل على رموز ، أو على جمل ، أو على متتابعات منتهية من الجمل . وبذا صار بإمكانه أن يخبر عن الجمل ، بأن
يخبر عن الأعداد التي تدل عليها . فمثلا نجح جودل في أن يصوغ في لغته الرمزية جملة تقول « أ ، ك كذا وكذا وكذا » ،
بحيث يكون تفسير هذه الجملة في الإطار الطبيعي هو أن أ عدد يدل على جملة ، وك عدد يدل على متابعة منتهية من
الجمل ، هي برهان للجملة التي يدل عليها العدد أ ، انطلاقا من مجموعة المسلمات الإضافية ݥ .
أكثر من ذلك ، استطاع جودل أن يصوغ جملة حـ تفسيرها في الإطار الطبيعي هو :
لا يوجد برهان للجملة حـ انطلاقا
من مجموعة المسلمات الإضافية ݥ
أي أن الجملة حـ تتحدث عن نفسها بطريقة تذكرنا بالجملة التي تكذب نفسها ، التي تحدثنا عنها من قبل .
النتائج :
هل الجملة حـ صادقة في الإطار الطبيعي ، وهل هي بالتالي إحدى مبرهنات النظرية ݨ ؟ هل هي إحدى
مبرهنات النظرية ࢶ ؟
لنبحث الأمر . لنفرض أن حـ إحدى مبرهنات ࢶ . إذن حـ إحدى مبرهنات ݨ ، لأن ࢶ جزء من ݨ .
أيضاً ، فرضنا أن حـ إحدى مبرهنات ࢶ ، يعني أنه يوجد برهان للجملة حـ انطلاقاً من مجموعة المسلمات الإضافية
ݥ . من هذا نري أن حـ كاذبة في الإطار الطبيعي . ومن ثم فإن حَـ ( التي سنرمز بها إلى نفي حـ ) صادقة في الإطار
الطبيعي ، وبالتالي فإن حَـ إحدى مبرهنات ݨ . وعلى هذا فإن النظرية ݨ غير متسقة لأن كلا من حَـ ، ونفيها
حًـ ، من بين مبرهنات ݨ .
ملخص ما سبق هو :
إذا كانت حـ إحدى مبرهنات ࢶ ، فإن ݨ غير متسقة .
وبأخذ عکس النقيض - كما يقول المناطقة - نخلص إلى أن :
إذا كانت ݨ متسقة ، فإن حـ ليست إحدى مبرهنات ࢶ .
لنفرض الآن أن ݨ متسقة . إذن حـ ليست إحدى مبرهنات ࢶ . وهذا يعني أنه لا يوجد برهان للجملة حـ
انطلاقاً من مجموعة المسلمات الاضافية ݥ . من هذا نرى أن حـ صادقة في الاطار الطبيعي ، وبالتالي فإن حـ إحدى
مبرهنات ݨ . بإضافة هذا إلى النتيجة السابقة نصل إلى أنه :
إذا كانت ݨ متسقة ، فإن حـ إحدى
مبرهنات ݨ ، لكنها ليست إحدى مبرهنات ࢶ .
وعلى هذا فإن ݨ تختلف عن ࢶ . وبذا نكون قد أجبنا عن سؤال جودل الثاني بالنفي ، بفرض أن ݨ
متسقة .
ما سبق لا يكفي للاجابة عن السؤال الأول بالنفي هو الآخر . حقاً إننا نعرف الآن أن ݥ لا تولد ݨ ( بفرض
أن الأخيرة متسقة ) ، لكن أليس من الممكن تقوية ݥ ، بإضافة حـ أو غيرها إليها ، بحيث يكفي الناتج لتوليد ݨ ؟
لاحظ أننا هنا لا نبحث عن أية مجموعة مولدة للنظرية ݨ ، وإنما نبحث عن مجموعة فعالة تفي بالغرض . لكننا
نستطيع أن نفعل مع أية مجموعة فعالة - تشمل ݥ ، وتشتمل عليها ݨ - ما فعلناه مع ݥ ، لنثبت أنها لا تولد ݨ
( بفرض أن الأخيرة متسقة ) . ومن هذا يمكن أن نستنتج :
إذا كانت ݨ متسقة ، فإنه لا يمكن توليدها
بأية مجموعة فعالة من المسلمات الإضافية .
وبذا نكون قد أجبنا عن سؤال جودل الأول بالنفي هو الأخر ! ( بفرض أن ݨ متسقة ) .
هذه النتيجة الخطيرة ، التي تعني أننا لا نستطيع - عمليا - أن نقيم النظرية ݨ على مسلمات ، جديرة بأن نتوقف
عندها قليلا . هل المشكلة في المنطق ، أي في المسلمات المنطقية وقواعد الاستنتاج ، وبالتالي فإذا قوينا المنطق فقد تحل
المشكلة أم أن المشكلة في اللغة الرمزية التي اختارها جودل ، وبالتالي فحل المشكلة قد يكمن في تغيير اللغة ؟ أم ماذا ؟
للإجابة عن هذه الأسئلة ، علينا أن نتعامل مع مفهوم جديد ، هو « فعالية التولد » . سنقول لمجموعة من الجمل
إنها فعالة التولد ، إذا كان بالإمكان توليدها بطريقة ميكانيكية . أي إذا كانت هناك آلة ( كمبيوتر مثلا ) تولدها واحدة
فواحدة . وبالرغم من أن عملية التوليد قد تستمر إلى مالا نهاية ، فإن كل جملة يجب أن تظهر بعد فترة زمنية محدودة ،
طالت أم قصرت . وذلك مثل عملية العد ، فهي لا تنتهي أبداً ، لكن كل عدد سيأتي دوره في الظهور بعد فترة زمنية
محدودة .
من السهل أن نرى أن كل مجموعة فعالة ، لابد وأن تكون فعالة التولد ، ذلك لأنه يمكن التعرف عليها
ميكانيكياً ، والآلة التي تتعرف عليها ، يمكنها بتعديل بسيط - أن تولدها فما علينا إلا أن ندخل جمل اللغة كلها إلى الآلة
واحدة فواحدة . ونجعل للآلة فتحتين تخرج من أولاهما الجمل التي تتعرف عليها الآلة على أنها من مجموعتنا ، وتخرج
من الثانية بقية الجمل . وبذا تولد الآلة - بما يخرج من فتحتها الأولى - جمل المجموعة واحدة واحدة .
بالمثل يمكن إثبات أن أية نظرية مولدة بمجموعة فعالة من المسلمات الإضافية ، لابد أن تكون فعالة التولد . ذلك
لأنه توجد - في هذه الحال - آلة بإمكانها التعرف على البراهين . فما عليك إذن إلا أن تدخل إلى هذه الآلة جميع المتتابعات
المنتهية من الجمل ، واحدة فواحدة . اجعل للآلة فتحتين ، واطلب منها ، إذا ما تعرفت على متتابعة على أنها برهان ،
أن تخرج الجملة الأخيرة ( أي المبرهنة ) من أولى الفتحتين . أما بقية الجمل فتخرج من الفتحة الثانية . بذا تولد الآلة -
بما يخرج من فتحتها الأولى - مبرهنات النظرية واحدة واحدة .
يمكن أيضاً إثبات أن عكس المقولة السابقة صحيح ، أي أن أية نظرية فعالة التولد ، لابد وأن يكون بالإمكان
توليدها بمجموعة فعالة من المسلمات الإضافية . وعلى هذا فيمكننا إعادة صياغة سؤال جودل الأول كالتالي :
هل ݨ فعالة التولد ؟
هذا السؤال المعدل يكافيء السؤال الأول ، لكنه سؤال في « ميكنة » الحقائق ، وليس - کالسؤال الأول - في
المنطق .
إعادة الصياغة لن تؤثر في الإجابة . وبالتالي فالإجابة عن السؤال المعدل هي أيضأ بالنفي ( بفرض أن ݨ
متسقة ) . لكن الصياغة المعدلة تساعدنا على التعرف على أبعاد الموقف بطريقة أفضل . لقد سألنا آنفاً إذا ما كانت
المشكلة في المنطق ، أم في اللغة ، أم ماذا ؟ لنفرض أن اللغة باقية كما هي ، وأن ݨ متسقة ، تغيير المنطق ( المسلمات
المنطقية وقواعد الاستنتاج ) لن يغير من ݨ شيئا ، لأن الذي يحدد جملة ݨ ليس البرهان الذي يتوقف على المنطق ،
وإنما الصدق الذي لا يتوقف إلا على اللغة وإطار التفسير ، وعلى هذا فإن ݨ ستبقى كما هي ، وعلى وجه التحديد
ستبقى غير فعالة التولد ، مهما غيرنا المنطق . ومن ثم فالحل الوحيد للمشكلة هو أن نغير المنطق مما يسمح لمجموعة فعالة
من المسلمات الاضافية أن تولد نظرية غير فعالة التولد . وهذا ممكن إذا ما تنازلنا عن شرط الفعالية في مجموعة المسلمات
المنطقية أو عن شرط إمكان التعامل مع قواعد الاستنتاج بطريقة ميكانيكية . لكن لا هذا ولا ذاك مرغوب فيه . فالتنازل
عن الشرط الأول يعني أننا قد لا نتمكن من التعرف على مسلماتنا المنطقية ، والتنازل عن الشرط الثاني يعني أننا قد لا
نعرف متى أو كيف نطبق قواعد الاستنتاج .
بقى أن ننظر في تغيير اللغة . وهذا طبعاً ممكن ، وسيأتي بنتيجة سريعة ، إذ أن ݨ تتغير بتغير اللغة . غير أنه إذا
كانت اللغة الجديدة على نفس مستوى اللغة القديمة ، أو أقوى ( أي أقدر على التعبير ) ، فإن ݨ الجديدة لن تكون
فعالة التولد ، وبالتالي ستبقى المشكلة كما هي ، إن لم تزدد تعقيداً . أما إذا كانت اللغة الجديدة أضعف من اللغة
القديمة ، فإن ݨ قد تصير فعالة التولد ، أو حتى فعالة ، وبذا تكون مشكلتنا محلولة بالنسبة إلى هذه اللغات الضعيفة .
فعلى سبيل المثال إذا ما أضعفنا لغتنا بما لا يسمح لها بالحديث عن ضرب الأعداد ، أي أن اللغة الجديدة ستكون قادرة
على الحديث عن الأعداد وجمعها ، لكن ليس ضربها ، فإن ݨ ستصير فعالة ، وليست فقط فعالة التولد .
القارئ اليقظ لا بد وأن يكون قد لاحظ أننا في طيات تحليلنا السابق قد عالجنا سؤالا كنا قد تركناه مفتوحا حين
طرحناه . ألا وهو : هل توجد مجموعة غير فعالة ؟ إذ أن ݨ ( في اللغة الأصلية ) ليست فقط غير فعالة ، وإنما أيضاً
غير فعالة التولد ( بفرض أنها متسقة ) .
كتمهيد لبحث قضية اتساق ب ( السؤال الثالث ) نود أن نوضح أن التحليل الذي أجراه جودل في معرض
معالجته لسؤاله الثاني كان أعمق من تحليلنا ، وأنه بتعامله مع التركيب الداخلي الدقيق للجملة حـ قد استطاع أن يصل
إلى النتيجة الأقوى التالية :
إذا كانت ࢶ متسقة ، فإن حـ ليست إحدى مبرهناتها (*) .
بطريقة مشابهة لتلك التي جرت بها صياغة الجملة حـ ، يمكن صياغة جملة د تفسيرها في الإطار الطبيعي هو :
ࢶ متسقة .
وبذا يكون تفسير الجملة ( د ← حـ ) في الإطار الطبيعي هو (*) على وجه التحديد . وقد أوضح جودل أن
اثبات (*) يمكن تقليده في اللغة الرمزية لنصل إلى أن :
( د ← حـ ) إحدى مبرهنات ࢶ .
فإذا كانت :
د إحدى مبرهنات ࢶ .
فإننا نصل بقاعدة الفصل إلى أن :
حـ إحدى مبرهنات ࢶ .
وهذا يتعارض مع اتساق ࢶ ، كما تبين (*) . من هذا نخلص إلى النتيجة الهامة الآتية :
إذا كانت ࢶ متسقة ، فإن د ليست إحدى مبرهناتها .
وبالنظر إلى تفسير د في الإطار الطبيعي ، فإن هذا يعني أنه إذا كانت ࢶ متسقة ، فإنه لا يمكن إثبات ذلك
بالطرق المستخدمة لإثبات مبرهنات ࢶ .
من الطبيعي أن نسأل ماذا يحدث إذا ما أضفنا د إلى ࢶ ؟ نحصل على نظرية أقوى ، يمكننا فيها إثبات أن ࢶ
متسقة . لكن ما فعلناه مع ࢶ يمكن تكراره مع النظرية الجديدة ، وبالتالي لا يمكن إثبات أن النظرية الجديدة متسقة
( بفرض أنها كذلك ) بالطرق المستخدمة لإثبات مبرهناتها . وهكذا فالمشكلة تطل علينا برأسها من جديد ، ولكن في
ظروف أعقد . ونفس الشيء يسري على أية تقوية للنظرية ࢶ ، مادام يمكن توليدها بمجموعة فعالة من المسلمات
الإضافية .
وعلى هذا فلا يمكننا الاطمئنان إلى اتساق ࢶ ، ولا إلى اتساق كثير غيرها من النظريات الأساسية في
الرياضيات ، إذ أن اثبات هذا الاتساق يتطلب نظرية لا يقل شکنا في اتساقها عن شكنا في اتساق النظرية الأصلية
نفسها .
أرجو أن يكون قد اتضح الآن لماذا اهتم جودل بقضية اتساق ࢶ . أما عن لماذا لم يعر قضية اتساق ݨ نفس
الاهتمام ، فلعل ذلك لأنه كان مهتما بالنتائج السلبية ، أي بتوضيح أن قضية الاتساق تنطوي على مشكلة وبالتالي فمن
الأوجب أن يتعامل مع النظرية الأضعف ، أي ࢶ . وما دمنا غير متيقنين من اتساق ࢶ ، فإننا - من باب أولى - لن
نكون متيقنين من اتساق ݨ .
خاتمة :
تبين لنا النتائج السابقة بعض حدود المعرفة . وقضية حدود المعرفة مبحث فلسفي قديم . والجديد هو أن يسهم
العلم في علاجها ، وإن كان اسهامه في تبيان بعض الحدود الأخرى ، التي شغل بأمرها الفلاسفة منذ زمن طويل ، ليس
بنفس القدر من الجدة .
فبتطور النظرية الذرية على أسس علمية مقبولة خلال القرن التاسع عشر ، أسهم العلم في الإجابة عن سؤال
فلسفي قديم متعلق بحدود إمكان تقسيم المادة . وقد تجدد هذا الاسهام - الذي لم يكن أبدا كلمة أخيرة - خلال القرن
العشرين بفعل نظریات تركيب الذرة من جسيمات أولية ، ونظريات تركيب بعض الجسيمات الأولية مما يسمى
بالكوارك ، ونظريات تحول المادة إلى طاقة ، وظهور الأخيرة على شكل كمات . .
وقد بينت لنا نظرية النسبية ( عام ١٩٠٥ ) حدأ آخر ، هو حد السرعة . فإذا كانت سرعة أحد جسمين بالنسبة
للآخر أقل من سرعة الضوء في الفراغ في لحظة ما ، فلا يمكن أن تزيد عليها أبدا ، أي أن سرعة الضوء في الفراغ
( حوالي ۳۰۰ ألف كيلو متر في الثانية ) هي حد السرعة .
أما ميكانيكا الكم فقد أتتنا ( عام ۱۹۲۷ ) بمبدأ عدم التحدد ، القائل بأن مقدار عدم التحدد في موضع جسيم
ما ، مضروبا في مقدار عدم التحدد في زخمه ( أي كمية حركته ) لا يقل عن مقدار ثابت ( لا يتوقف على الجسيم . وقد
ذهب المشتغلون بالفيزياء وفلسفتها في تفسير هذا المبدأ مذهبين . يقول الأول إن عدم التحدد خاصة موضوعية من
خواص موضوع المعرفة ، وبالتالي فهو لا يضع قيدا على المعرفة . وعلى هذا تكون نتائج جودل أول نتائج علمية متعلقة
بحدود المعرفة . ويرجع المذهب الثاني عدم التحدد إلى الذات العارفة والأجهزة التي تستخدمها ، وبالتالي فهو يعتبره
قيداً على المعرفة . وعلى هذا يكون مبدأ عدم التحدد هو أول النتائج العلمية المتعلقة بحدود المعرفة ، ونتائج جودل هي
الثانية .
وسواء أكانت نتائج جودل هي الأولى أم الثانية ، فعلينا أن نتفهم أبعادها . ولنبدأ بالنتيجة القائلة بأن ݨ ليست
فعالة التولد . هذه النتيجة تعني أنه لا يمكننا معرفة كل الحقائق المتعلقة بالأعداد . وَرُبَ قائل : أما كان يكفي إثبات أن
ݨ لا نهائية ؟ فمعرفتنا - مهما زادت - ستظل محدودة ، وبالتالي لا يمكننا معرفة كل الحقائق المتعلقة بالأعداد ، إذا كانت
لا نهائية . الجواب : نعم ، ما كان يكفي . فنحن قادرون - بمعني معقول جدا - على معرفة عدد لا نهائي من الحقائق .
ألسنا نعرف أن ۱ + ۱ = ۲ ، ۱ + ٢ = ۳ ، . . . ، ۱ + ۸ = ۹ ، ۱ + ۹ = ۱۰ ، . . . ، ۱ + ۸٤ = ۸٥ ، . . .
وهكذا إلى مالا نهاية ؟ أكثر من هذا ، نستطيع أن نقول إننا نعرف أية مجموعة فعالة ، متى توصلنا إلى آلة قادرة على
التعرف عليها . لأننا في هذه الحال - ما علينا إذا ما أعطينا جملة من الجمل إلا أن نضعها في الآلة التي ستقف بعد فترة
محدودة من الزمن قائلة لنا إذا ما كانت الجملة في مجموعتنا أم لا . يرد هنا اعتراض على القيمة العملية لهذه المعرفة . إذ
أن الآلة قد تستمر في العمل مليون سنة قبل أن تصدر حكمها على جملة ما . بالرغم من وجاهة هذا الاعتراض ،
فسيظل بإمكاننا أن نقول إننا نعرف ، على الأقل نظرياً ، على الأقل من حيث المبدأ .
يصير الأمر أكثر تعقيداً إذا كانت لدينا نظرية فعالة التولد ، لكنها ليست فعالة . في هذه الحال لا توجد آلة قادرة
على التعرف على جمل النظرية ، وإنما توجد آلات قادرة على توليدها فقط . لنفرض أن لدينا إحدى هذه الآلات ، وأن
لدينا جملة ما ، لا نعرف إذا ما كانت في النظرية أم لا . إذا كانت الجملة في النظرية ، فإنها ستخرج من الآلة بعد وقت
طال أم قصر . وبالتالي فسنعرف أنها في النظرية . أما إذا لم تكن في النظرية ، فإنها لن تخرج من الألة مهما طال
انتظارنا ، وفي نفس الوقت لن تصدر الماكينة حكما بأنها لن تخرج أبدا . الآلة إذن لن تحسم الأمر ، وبالتالي فإن فائدتها ۔
مهما عظمت - ستكون جزئية فقط .
يمكننا أن ننظر إلى الأمر بشكل آخر . فلكل نظرية فعالة التولد توجد مجموعة فعالة من المسلمات الإضافية
المولدة . فإذا ما وضعنا يدنا على مجموعة فعالة مولدة ، فإننا سنعرف الكثير عن النظرية . ذلك لأنه سيوجد لكل جملة في
النظرية برهان انطلاقاً من هذه المجموعة الفعالة ، ومن ثم فإن مفهوم البرهان سيصير أوضح وأبسط کا بینا آنفاً . وهذا
سيسهل التعامل مع البراهين ، سواء أكنا نحاول برهنة جملة ما ، أم نحاول إثبات عدم وجود برهان لها ، وإن كان لا
يوجد ما يضمن نجاح هذه المحاولات . على كل هذه النظرة تكافيء النظرة السابقة ، كما أشرنا من قبل .
هل لنا إذن أن نقول إننا نعرف النظرية فعالة التولد ، إذا ما عرفنا آلة تولدها ؟ هذه مسألة فيها نظر. ويبدو أنه مما
يساعد على حلها أن نأخذ بأن المعرفة مفهوم مركب ، وبدلا من أن نسأل ، هل نعرف ؟ أو ، هل يمكن أن نعرف ؟
نسأل إلى أية درجة نعرف ؟ أو ، إلى أية درجة يمكن أن نعرف ؟ إذا ما قبلنا هذا ، فإن التحليل السابق ( وهو الآن يحتاج
إلى شيء من التعديل الذي سنتركه للقارىء ) يجيز لنا أن نقول إنه ليس بإمكاننا أن نعرف النظريات فعالة التولد ( التي
لیست فعالة ) بنفس الدرجة التي يمكننا أن نعرف بها النظريات الفعالة . أي أن هناك حدوداً للمعرفة !
لكن هل توجد نظرية فعالة التولد ، لكنها ليست فعالة ؟ نعم ، وأول نظرية عرف عنها هذا هي النظرية ࢶ
( بفرض أنها متسقة ) . وعلى هذا فالمشكلة تبدأ من ࢶ ، لكن مشكلة ݨ أكبر ، لأن ݨ ( بفرض اتساقها ) ليست
حتى فعالة التولد . ولذا فإن درجة معرفتنا بالنظرية ݨ لا يمكن أن تصل حتى إلى الدرجة التي يمكن أن تصل إليها
معرفتنا بالنظرية ࢶ . فمثلا نحن نعرف للنظرية ࢶ مجموعة ( فعالة ) من المسلمات الإضافية التي تولدها ، وهذا
مالا يمكننا أن نعرفه للنظرية ݨ .
وكما أسلفنا فإن من أوجه قصور معرفتنا بالنظرية ࢶ ، أننا لن نعرف طريقة عامة ( أي لن نتوصل إلى آلة )
نستطيع عن طريقها أن نحكم على كل جملة إذا ما كانت في ࢶ أم لا . إن وجه القصور هذا قائم ( بل انه أكثر شدة ،
إن جاز التعبير ) بالنسبة للنظرية ݨ . وبهذا المعنى نقول إننا لا يمكننا معرفة كل الحقائق المتعلقة بالأعداد ( أي كل
الجمل الواقعة في ݨ ) .
أصابت هذه النتيجة البعض بشيء من خيبة الأمل . لكنها لا تخلو من جانب مشوق . فهي تزيد من التحدي ،
وبالتالي تزيد من استثارة الهمم . فالنتيجة لا تقول إن هناك جملة بعينها غير قابلة لأن نحكم عليها . إنها تقول فقط إنه لا
توجد طريقة واحدة صالحة للحكم على كل الجمل . وبالتالي علينا دائما أن نبتكر طرقاً جديدة . وهذا خلیق بأن يرضي
غرور الرياضيين ، إذ أن الحاجة إلى ابتكاراتهم لن تنتهي ، ولن يمكن الاستعاضة عنهم بآلة ، أو بكمبيوتر أبدا .
لقد راود الرياضيين أمل بأن تكون مسلمات بيانو ( المشار إليها آنفاً ) كافية لبرهنة كل الحقائق المتعلقة بالأعداد .
فبدد جودل هذا الأمل بنتيجته العبقرية . لكنه لم يتركنا حائرين بعد أن أخرجنا من نعيم الجهل ( وأخو الجهالة في
الشقاوة ينعم ! ) . إذ أنه بإثباته أن حـ تقع في ݨ ولا تقع في ࢶ ، فتح لنا الطريق كي نحصل على نظرية أقوى
باضافة حـ ( أو غيرها من الجمل التي تقع في ݨ ولا تقع في ࢶ ) إلى المسلمات الاضافية التي تقوم عليها ࢶ .
وهكذا يمكننا أن نحصل على نظريات أقوى وأقوى ( تقوم كل منها على مجموعة فعالة من المسلمات الإضافية ) دون أن
نصل إلى ݨ أبداً . أي أن دائرة الضوء تتسع وتتسع ، لكنها لن تضيء كل الحقائق أبدا . أيضاً ، فتح لنا جودل
بنتيجته هذه طرقاً أخرى ، لكن المجال لا يسمح لنا باصطحاب القاريء إلى جولة فيها .
لننتقل الآن إلى نتيجة جودل الثانية القائلة بأنه إذا كانت ࢶ متسقة ، فإنه لا يمكن إثبات ذلك بالطرق
المستخدمة لإثبات مبرهنات ࢶ . هذه النتيجة لا تعني أن ࢶ ليست متسقة ، كما أنها لا تعني أن ࢶ متسقة . فهی
تترك الباب مفتوحا لهذا وذاك . كل ما نستطيع أن نبنيه عليها هو أنه إذا كانت ࢶ متسقة ، فإننا لن نستطيع معرفة هذا
بطريقة نطمئن إليها .
زادت هذه النتيجة من شكوك أصحاب الاتجاهين الحدسي والبنائي ( وهما اتجاهان في الرياضيات وفلسفتها
ازدهرا في بدايات هذا القرن استجابة للأزمة التي شهدتها الرياضيات مع دورة القرن التاسع عشر ) في سلامة
الرياضيات التقليدية . وشجعتهم على الاستمرار في جهودهم لإقامة رياضيات جديدة أكثر جدارة بالثقة ، لكنها - حتى
الآن - أقل فائدة في التطبيق .
أما الغالبية الساحقة من الرياضيين ومستخدمي الرياضيات ، فتسير أمورهم سيراً عادياً فهم ليسوا بحاجة إلى
اليقين حتى يستمروا في بحثهم ودرسهم وتدريسهم وتطبيقاتهم . والتعامل مع النظرية ࢶ مستمر ، والبحث فيها
وحولها جار . لكن أحدا لن يذهل إذا ما اكتشف فيها تناقضاً غدا . حقا إن هذا سيكون حدثاً عظيماً ، وسيدخل
الرياضيات في أزمة جديدة . لكن المأمول أن تكون - كسابقاتها - أزمة نمو ، لا أزمة انهيار .
هل نتيجة جودل ، التي زعزعت اليقين في الرياضيات ، نتيجة يقينية ؟ لقد توصل إليها جودل بنفس
الأساليب ، وعلى نفس الأسس ، التي هي الآن موضع شك . إذن فالنتيجة نفسها موضع شك . أي أن الشك الذي
توصلنا إليه هو في حد ذاته أمر مشكوك فيه . ولذا فاستعادة اليقين أمر وارد ، وإن كان ليس متوقعاً إلا من خلال تغير
جذري في مفاهيمنا الرياضية . والمقصود هنا ، هو استعادة اليقين بمعظم الرياضيات التقليدية ، وليس بالرياضيات
الحدسية أو البنائية ( انظر عاليه ) ، التي لم يدع أحد - حتى الآن - بأنها موضع شك .
ما شأن كل هذا بمعرفة الكون ؟ لعل هذا هو أكثر ما يعني المشتغلين بالعلوم الطبيعية والبيولوجية والإنسانية ،
وفلسفاتها . لنلاحظ أولا أن كون الاطار الطبيعي ( الذي يضم كل الأعداد الطبيعية ) لا نهائي قد لعب دوراً لا غنى عنه
في طهور المشكلات السابقة . ولو لم يكن الأمر كذلك ، أي لو كان الإطار الطبيعي محدودا ، ما نشأت هذه
المشكلات . بل وما كان هناك فرق بين الرياضيات التقليدية والرياضيات الحدسية والبنائية . وعلى هذا فعلاقة نتائج
جودل بمعرفة الكون تتوقف على ما إذا كان الكون لانهائياً . وفي نقاشنا التالي لعلاقة المواقف الثلاثة الممكنة من قضية
لانهائية الكون بنتائج جودل ومشكلة المعرفة ، سنفهم « الكون » بالمعنى الواسع الذي يسمح باعتبار الظواهر الإنسانية
ظواهر كونية . أيضاً ، ما نقوله عن الكون يمكن أن يقال عن أي جزء من أجزائه ، أو أي جانب من جوانبه .
(۱) الكون لا نهائي :
إذا كان الكون لا نهائياً ، في أي وجه من وجوهه ، فالمتوقع أن يكون أعقد من الإطار الطبيعي ( أي الأعداد
الطبيعية مع الجمع والضرب ) ، وبالتالي فمن المتوقع أن تسري عليه نتائج جودل . أي أن مجموعة الحقائق الكونية لا
يمكن استنتاجها من مجموعة فعالة من المسلمات ، وأنه لا يمكن الاطمئنان إلى اتساق أية نظرية كونية قوية .
(۲) الكون محدود :
المقصود هنا أن يكون الكون محدوداً من جميع الوجوه . أي أن يكون مكوناً من عدد محدود من الأشياء ، لكل منها
عدد محدود من الصفات ، وتدخل في بعضها البعض في عدد محدود من العلاقات الثنائية ، كما تدخل مع بعضها البعض
في عدد محدود من العلاقات الثلاثية ، وهكذا ، على أن يكون عدد كل العلاقات محدودا . وأيضاً أن يكون محدوداً في
الزمان ، بمعنى أنه لا يمر إلا بعدد محدود من الأطوار ، ثم يثبت أو ينتهي أو يعيد الكرّة .
في هذه الحال نتائج جودل غير واردة بالنسبة إلى الكون . ومجموعة الحقائق الكونية لن يكون من الممكن فقط
استنتاجها من مجموعة فعالة من المسلمات ، بل ستكون هي نفسها مجموعة فعالة . ولن تكون هناك مشكلة في إثبات
اتساق النظرية المكونة من الحقائق الكونية كلها . والتوصل إلى هذه النظرية أمر وارد نظرياً ، غير أن هذا شيء ،
والتوصل إليها فعلا شيء آخر. وحتى إذا توصلنا إليها فعلا ، فقد يتعذر علينا التأكد من هذا .
ورغم أن المجال لا يسمح بالخوض في مزيد من التفصيلات ، فقد يكون من المفيد أن نذكر هنا أن مشكلة
الاستقراء التي أثارها ديفيد هيوم سيكون من السهل حلها في حالنا هذه . إذ أن عدد كل ما لدينا من أشياء محدود ،
وبالتالي فمن الممكن أن يكون الاستقراء دائماً استقراء کاملا .
(3) الكون آخذ في الاتساع :
المقصود أن يكون الكون - حتى كل لحظة - محدودا بالمعنى الوارد في (۲) ، لكن الحدود متحركة ، كلها أو
بعضها . كأن يكون عدد الأشياء التي يتكون منها الكون اليوم مليوناً ، ويصير غداً مليوناً وألفاً ، وهكذا .
وفي هذه الحال ، يبدو أن الرياضيات الحدسية أو البنائية ستكون كافية لدراسة الكون ، ويكون استخدامنا الحالي
للرياضيات التقليدية نوعاً من الاستسهال . أي أن لنا أن نختار بين رياضيات أصعب في التعامل ، لكنها أجدر بالثقة ،
وبين رياضيات أسهل في التعامل ، لكنها تعاني من كل المشكلات التي أوضحها جودل(**) .
المراجع
(1) Godel Kurt; On Formally Undecidable Propositions of Principia Mathematica and Related Systems; Basic Books Inc. New York, 1962.
(2) Hofstadter, Douglas R.; Godel, Escher, Bach: An Eternal Golden Braid, Vintage Books, New York, 1980.
(3) Kleene, Stephen Cole; Mathematical Logic; John Wiley and Sons, Inc. New York, 1967.
(4) Mendelson, Elliott; Introduction to Mathematical Logic; D. Van Nostrand Company, Inc. Princeton, New Jersey, 1964.
(5) Nagel, Ernest and Newman, James R.; Godel's Proof; New York University Press, . 1964.
(6) Sagan, Carl; Cosmos; Random House, New York, 1980.
(7) Taraki, Alfred; The Concept of Truth In Formalized Languages; In; Logic, Semantics, Metamathematics; By the same author, Oxford At The Clarandon Press, 1956.
(8) ——— ; Truth and Proof; Scientific American, June 1969. Also, republished in: Fundamental Problems In Philosophy; Edited by Oswald Hanfling; Basil Black-well In Associations with The Open University Press, 1972.
المرجع (۱) ترجمة للبحث الأصلي لجودل ، مصحوبة بمقدمة مبسطة .
المراجع (۳) ، (٤) ، (۷) مكتوبة للمتخصصين . المرجع (۷) بحث له أهمية تاريخية فيما يتعلق بقضية الصدق .
والمرجعان (۳) ، (٤) كتابان جامعيان يغطي كل منها : اللغات الرمزية ، البرهان ، الصدق ، نتائج جودل .
المراجع (۲)، (ه) ، (٦) ، (۸) مكتوبة لغير المتخصصين . وكلها - عدا (٦) - تستعرض وتناقش نتائج
جودل . المرجع (۲) يربطها بالرسم والموسيقى ، والمرجع (۸) يركز أكثر على قضيتي الصدق والبرهان . أما المرجع (٦)
فيبحث في الكون وفهمنا له .
(*) هذا المقال مهدى إلى السيد الأستاذ الدكتور مصطفى سويف تحية لجهوده في ضبط العلوم الإنسانية ، وبمناسبة تجاوز سيادته سن الستين .
(١) في هذا المقال سنستخدم الكلمتين « منتهي » و « محدود » بمعنى واحد، هو ليس لا نهائيا .
(۲) ما نفعله هنا ليس بالضبط ما فعله جودل ، فسنسمح لأنفسنا بالاستفادة من التطورات التي جرت بعد ١٩٣١ كما أننا نبسط الأمور كثيراً، بعدا بالقارئ عن التعقيدات الفنية .
(**) لكن ما رأي علماء الكون في قضية لا نهائيته ؟ الإجابة عن هذا السؤال خارج نطاق هذا المقال ، ويمكن للقارئ أن يرجع فيها إلى المرجع رقم (٦) ، حيث سيجد المزيد من المراجع .
المصدر: مجلة عالم الفكر - المجلد العشرون - العدد الرابع - يناير - فبراير - مارس ١٩٩٠ م
,%20%2340884,%20Egypt%20(ar)_0062.jpg)