حلت الحضارة البابلية في بلاد ما بين النهرين محل الحضارة السومرية والحضارة الأكادية. غطينا القليل عن الخلفية التاريخية لهذه الأحداث في مقالتنا الرياضيات البابلية. ورث البابليون من السومريين والأكاديين الأفكار المتعلقة بنظام الأعداد. جاء استخدام 60 كقاعدة (أي النظام الستيني) من أنظمة أعداد هذه الشعوب السابقة. ومع ذلك، لم يكن النظام العددي السومري ولا الأكادي نظامًا موضعيًا والتطور الذي أدخله البابليون كان بلا شك أعظم إنجازاتهم في النظام العددي. وقد يجادل البعض بأنه كان أكبر إنجازاتهم في الرياضيات.
غالبا عندما يُقال أن نظام الأرقام البابلي كان ستيني القاعدة فإن أول رد فعل هو: لا بد أنه كان عليهم تَعَلُّم الكثير من الرموز الخاصة بالأعداد. بالطبع رد الفعل هذا سببه معرفتنا بنظامنا العشري وهو نظام موضعي به تسعة رموز خاصة ورمز للصفر يشير لخلو الموضع من أي قيمة. ومع ذلك، فبدلاً من الاضطرار لتعلم 10 رموز كما نفعل لاستخدام الأعداد العشرية، كان على البابليين تعلم رمزين فقط.
برغم أن النظام البابلي كان نظامًا موضعيًا ستينيًا، إلا أنه حوى آثار من النظام العشري. وذلك لأن الـ 59 رقما المستخدمة فيه، تتكون من رمز "للوحدة" ورمز "للعشرة".
وهاك الـ 59 رقما ممثلة بهذين الرمزين
 |
| رموز الأرقام البابلية |
في نظام الأرقام الموضعي نحتاج لمعرفة أي طرف (يمين أم يسار العدد) يمثل عدد الوحدات. كمثال خذ العدد العشري 12345 ويُمَثَّل بـ
1×104+2×103+3×102+4×10+5.
لو فكرنا لبرهة، لربما بدا هذا غير منطقي لأننا نقرأ العدد من اليسار لليمين، ولذا لن نعرف قيمة أول رقم حتى نقرأ العدد بالكامل لمعرفة عدد الخانات لنعرف قوة المكان الأول العشرية (في المثال السابق خمس خانات وعليه يكون المكان الأول من خانة عشرات الآلاف وهكذا ... الخ). يستخدم النظام الستيني البابلي نظاما مشابها، فالأرقام على أقصى اليمين تأخذ قيما من الواحد حتى 59، وعلى يساره تأخذ قيمة (60×n) حيث (1≤n≤59)، وهكذا. دعنا الآن نكتب العدد وفيه بين كل رقم والتالي له فاصلة، كمثال ، 1 ، 57 ، 46 ، 40 يمثل العدد الستيني
1×603+57×602+46×60+40
وهو ما يكافئ 424000 بالنظام العشري.
هنا 1 ، 57 ، 46 ، 40 بنظام الأعداد البابلية
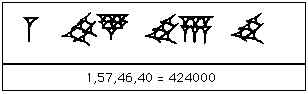 |
| العدد 424000 بنظام الأرقام البابلي |
الآن توجد احتمالية حدوث خلط في تمثيل الأعداد في هذا النظام، خذ على سبيل المثال العددين 2 و 61، الأول (وهو الرقم 2) سيٌمَثَّل بشكلين كل واحد منهم يرمز للواحد، والثاني (وهو الرقم 61 وبالترميز هنا يكون 1,1) سيٌمَثَّل بشكل يرمز للواحد في أول موضع (موضع الآحاد في النظام الستيني)، وبشكل آخر يرمز للواحد أيضا ولكن في الموضع التالي (موضع مضاعفات الستين). ولكن لم تكن هذه مشكلة حقًا لأن المسافات بين الأشكال سمحت بتمييز الفرق. ففي حالة العدد 2، يتلامس الشكلان الممثلان للواحد ليصبحا كأنهما رمزًا واحدًا (راجع الجدول بالأعلى). في حالة العدد 61 فإن الرمزين 1 و 1 بينهما مسافة كافية لتمييزهما عن العدد 2.
المشكلة الأكبر كانت في غياب رمز الصفر في المواضع الخالية. فالعدد الستيني 1 (= 1 في النظام العشري) و "1 ، 0" (= 60 في النظام العشري)، لهما نفس التمثيل بالضبط ولن تنفع المسافات في التمييز بينهما هنا. يمكن التمييز بينهما بناءا على سياق الاستخدام، ولو بدا لنا هذا غير مُقْنِع، فإن البابليين كانوا مقتنعون به. كيف عرفنا هذا؟ حسنًا ، لأنهم لو كانوا وجدوا مشاكل في هذا النظام، لقاموا بمحاولة حلها - ولديهم مهارات كافية بلا شك للوصول لحل عملي. علينا أن نَذْكُر هنا أن الحضارة البابلية فيما بعد اخترعت رمزًا للإشارة لخلو الموضع، وهو دليل على أن غياب الصفر لم يكن مُرضيًا لهم.
تسبب خلو الموضع في منتصف العدد بمشاكل. وبرغم أن الملاحظة التالية ليست جادة تماما، لكن جدير بالملاحظة أنه في نظامنا العشري بافتراض تساوي احتمال تواجد جميع الأرقام العشرية، فهناك احتمال واحد من عشرة لموضع خالي، ينما لنظام البابليين الستيني، هناك احتمال واحد من ستين. بالعودة للمواضع الفارغة في منتصف العدد، لنلق نظرة على أمثلة فعلية لهذا.
هذا مثال من لوح مسماري (في الواقع AO 17264 من مجموعة اللوفر في باريس) وفيه حساب تربيع العدد 147 . بالستيني 147 = 2 ، 27 وتربيعه يعطي 21609 = 6 ، 0 9 .
وهاك تربيع 2 ، 27 في النظام البابلي
 |
| تربيع بابلي |
لعل الكاتب ترك مسافة أكبر قليلاً من المعتاد بين الـ 6 و 9 مما كان سيفعله لو كان يمثل 6 ، 9 .
الآن لو سببت هذه المسافة مشكلة للأعداد الصحيحة، فستسبب مشكلة أكبر للكسور الستينية البابلية.
استخدم البابليون نظام كسور ستيني مشابه للكسور العشرية. كمثال لو كتبنا 0.125 وتُمَثل كسريًا على هذا النحو
1/10 + 2/100 + 5/1000 = 1/8.
بالطبع كسر بصيغة a/b ممثل بأصغر القيم، يمكن كتابته ككسر عشري محدود إذا وفقط إذا لم يكن لـ b أي قواسم أولية غير 2 أو 5. لذا لا يوجد كسر عشري محدود لـ 1/3. وبالمثل فإن الكسر الستيني البابلي 0 ؛ 7 30 ممثلًا بـ 7/60 + 30/3600 يقابله بالنظام العشري 1/8.
وبما أن 60 قابلة للقسمة بالأعداد الأولية 2 و 3 و 5 فإن كسر بصيغة a/b ممثل بأصغر القيم، يمكن تمثيله ككسر عشري محدود إذا وفقط إذا لم يكن لـ b أي قواسم أولية غير 2 أو 3 أو 5. لذا يمكن تمثيل الكثير من الكسور ككسور ستينية منتهية أكثر منها ككسور عشرية منتهية. يعتقد بعض المؤرخين أن هذا سبب مباشر لاستخدام البابليين للنظام الستيني، بدلاً من النظام العشري، لكن ليس بشكل مؤكد، لأنه لو كان هذا صحيحا فلما لم يستخدموا 30 كأساس؟ سنناقش هذه المسألة ببعض التفصيل بالأسفل.
كنا قد أشرنا للطريقة التي سنستخدمها لكتابة عدد ستيني له جزء كسري. للتوضيح 10 ، 12 5 ؛ 1 ، 52 ، 30 يكتب بالنظام الستيني هكذا
10×602+12×60+5+601+60252+60330
وهو ما يقابل 36725 1/32 بالنظام العشري.
كل هذا جيد، ولكن لاحظ أننا استخدمنا فاصلة منقوطة كعلامة على انتهاء الجزء الصحيح وبداية الجزء الكسري. هذه "النقطة الستينية" (الفاصلة المنقوطة) تقوم بنفس وظيفة النقطة العشرية. ولكن لم يكن لدى البابليين أي علامة لتحديد نهاية الجزء الصحيح وبداية الجزء الكسري. ومن هنا جاءت صعوبة فهم بعض الأرقام وفشلت فلسفة "أن السياق سيوضح المعنى" في إزالته بشكل كبير.
لو كتبنا 10 ، 12 ، 5 ، 1 ، 52 ، 30 بدون "النقطة الستينية"، فقد يعني ذلك أيًا مما يلي:
0 ؛ 10 ، 12 ، 5 ، 1.52 ، 30
10 ؛ 12 ، 5 ، 1،52 ، 30
10 ، 12 5 ، 1،52،30
10 ، 12 ، 5 ؛ 30 52 1
10 ، 12 ، 5 ، 1 ؛ 52،30
10 ، 12 ، 5 ، 1.52 ، 30
10، 12، 5، 1،52 30
هذا بالطبع بالإضافة لـ 10 أو 12 أو 5 أو 1 أو 52 أو 30 أو 0 أو 0 ؛ 0 ، 10 ، 12 ، 5 ، 1 ، 52 ، 30 إلخ.
وأخيرًا ، سنبحث هنا مسألة استخدام العدد 60 كأساس لنظام الأرقام البابلي. الجواب السهل هو أنهم ورثوا الأساس الستيني من السومريين ولكن هذا ليس جواباً على الإطلاق. لأننا لم نعرف لم استخدم السومريون العدد 60 كأساس. أول نقطة هو أنه ليس علينا العودة للوراء أبعد من هذا لأننا متأكدين من أن النظام الستيني نشأ مع السومريين. النقطة الثانية الواجب توضيحها هي أن علماء الرياضيات الحديثين لم يكونوا أول من طرح مثل هذه الأسئلة. فثيون السكندري حاول إجابة هذا السؤال في القرن الرابع بعد الميلاد، والعديد من مؤرخي الرياضيات حاولوا منذ ذاك الحين دون إجابة مقنعة.
إجابة ثيون كانت أن 60 هو أصغر عدد يقبل القسمة على 1 و 2 و 3 و 4 و 5، وهذا من شأنه تكثير عدد القواسم. وبرغم صحة هذا الرأي، إلا أنه يبدو أكاديميًا بشكل كبير. لأنه لو كان هذا هو السبب فالعدد 12 كأساس يبدو مناسبا جدا لهذا الغرض، ومع هذا لا يبدو أن أي حضارة كبرى قد استخدمت العدد 12 كأساس. وم ناحية أخرى استخدم العدد 12 في العديد من المقاييس، كالأوزان والمال والأطوال. ففي المقاييس البريطانية القديمة كمثال كان هناك 12 بوصة في القدم، و 12 بنسًا في الشلن ، إلخ.
اقترح نيجوبار نظرية تستند لأوزان ومقاييس السومريين. أساس فكرته أنهم تحولوا من نظام عد عشري لأساس ستيني لتسهيل قسمة الأوزان والمقاييس لأثلاث. نعلم يقينا أن نظام أوزان ومقاييس السومريين استخدم بالفعل 1/3 و 2/3 ككسور أساسية. ومع ذلك، وبرغم أن نيجوبار قد يكون صحيحًا، إلا أن الحجة المضادة ستكون أن نظام الأوزان والمقاييس كان نتاج لنظام الأرقام وليس العكس.
نظريات عدة استندت على الأحداث الفلكية. فهناك اقتراح غير مُقنِع بأن سبب استخدام 60 كأساس لأنه حاصل ضرب عدد الأشهر في السنة ( عدد الأقمار في السنة ) مع عدد الكواكب ( عطارد ، الزهرة ، المريخ ، المشتري ، زحل ). اقترح مؤرخ الرياضيات موريتز كانتور أن طول العام والمعروف وقتها بـ 360 يومًا كان السبب لاستخدام 60 كأساس. وهو أيضا اقتراح غير مُقنِع لأن السومريين عرفوا بالتأكيد أن العام كان أطول من 360 يومًا. فرضية أخرى اعتمدت على أن مسار الشمس في السماء يقطع 720 قوسًا في اليوم، ومع 12 ساعة سومرية في اليوم، نحصل على العدد 60 (720/12).
اعتمدت نظريات أخرى على الهندسة. كمثال تقول إحدى النظريات أن السومريين اعتبروا المثلث متساوي الأضلاع أساسا لهندستهم. ومعروف أن زاويا مثلث متساوي الأضلاع هي 60 درجة، لو قسمناها على 10، ستكون 6 درجات هي الوحدة الزاويّة الأساسية. وفي الدائرة لدينا ستون وحدة من هذه الوحدات الأساسية، وهذا سبب استخدام 60 كأساس. لاحظ التناقض في هذه النظرية لأنها تفترض العدد 10 كأساس للقسمة!
أنا [ E F Robertson (أحد مؤلفي هذه المقالة) ] أشعر أن كل هذه النظريات لا تستحق أخذها بجدية. وربما بسبب أنني كونت رأيي الخاص بي، لكني عندما أقول جملة "اختيار 60 كأساس" فإنها تعني الكثير. أنا فقط لا أعتقد باختيار أي شخص للأساس العددي لأي حضارة. هل بإمكانك تخيل أن السومريين شكلوا لجنة لاختيار الأساس العددي - لا تحدث الأشياء بهذه الطريقة. لا بد أن يتضمن السبب نشأة طرق العد في الحضارة السومرية ، كما حدث في الحضارات الأخرى عندما أصبحت العشرة أساس لأنهم استخدموا أصابع اليد العشرة للعد، وأصبحت العشرون أساس لمن عَدّوا على أصابع اليدين والقدمين.
هذا اقتراح لكيفية حدوث هذا. يمكن العد حتى 60 باستخدام اليدين. على أصابع اليد اليسرى (عدا الإبهام) توجد ثلاثة أجزاء. يقسم هذه الأجزاء مفاصل الأصابع. الآن يمكن العد حتى 60 لو استخدمنا أي اصبع من أصابع اليد اليمنى الخمسة للإشارة لأي جزء من هذه الأجزاء الاثنى عشر على اليد اليسرى. وتكون هذه طريقة عد الأصابع حتى 60 بدلاً من 10 . أي شخص مُقتَنِع؟
نظرية مغايرة اقترحها آخرون. وربما هي النظرية الأكثر قبولًا واقترحت أن الحضارة السومرية ربما نشأت نتيجة لانضمام شعبين، أحدهما استخدم 12 كأساس للعد والأخر الأساس 5 . وبرغم أن الرقم 5 لم يكن شائعًا بين الشعوب القديمة كالـ 10 كأساس للعد، إلا أنه أُستخدم من قِبَل أناس يعدون على أصابع اليد الواحدة ثم يعيدوا الكَرَّة. بعد ذلك تفترض هذه النظرية أنه باختلاط الشعبين ووجود نظامي عد مستخدمين في التجارة بين الشعبين، فإن الأساس الستيني نشأ كحل طبيعي مفهوم للطرفين.
سمعت بنظرية مقترحة بنفس الفكرة ولكن باختلاف بسيط، فالشعبين الذين اختلطوا ليظهر منهم السومريون كانا يستخدمان الـ 10 و 6 كأساس للعد. ميزة هذه النسخة وجود مكان طبيعي للـ 10 في النظام البابلي، والتي ربما جدلًا هي من بقايا النظام العشري السابق. ميزة وجمال هاتان النظريتان في أنه يمكن العثور على دليل مكتوب لوجود نظامين اختلطا، وبالتالي تقديم ما يمكن اعتباره دليلا على صحتهما. لا تنظر للتاريخ باعتباره موضوع منتهي. بل عكس ذلك، تتغير مفاهيمنا باستمرار مع الأبحاث الحديثة التي تُظهِر للضوء أدلة وتفسيرات جديدة.
المصادر:
- A Aaboe, Episodes from the Early History of Mathematics (1964).
- R Calinger, A conceptual history of mathematics (Upper Straddle River, N. J., 1999).
- G Ifrah, A universal history of numbers : From prehistory to the invention of the computer (London, 1998).
- G G Joseph, The crest of the peacock (London, 1991).
- O Neugebauer and A Sachs, Mathematical Cuneiform Texts (New Haven, CT., 1945).
- B L van der Waerden, Science Awakening (Groningen, 1954).
- B L van der Waerden, Geometry and Algebra in Ancient Civilizations (New York, 1983).
- J Hoyrup, Babylonian mathematics, in I Grattan-Guinness (ed.), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences (London, 1994), 21-29.
- J Friberg, Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations, Historia Mathematica 8 (1981), 277-318.
📗 طالع أيضاً:
- طالع ترجمة لمقالة نظام الأرقام العربية.
- طالع ترجمة لمقالة الأرقام الهندية.
- طالع ترجمة لمقالة تاريخ الصفر.
- طالع ترجمة لمقالة الأرقام المصرية.
- طالع ترجمة لمقالة رياضيات المايا.
- طالع ترجمة لمقالة أنظمة الأرقام اليونانية.
ليست هناك تعليقات:
إرسال تعليق