أنظمة الأرقام اليونانية

المقالة هنا ترجمة بتصرف لمقالة بعنوان Greek number systems من تأليف: J J O'Connor  و E F Robertson

في الألفية الأولى قبل الميلاد لم تُوجَد معايير يونانية وطنية موحدة. لأن ولايات الجزر المختلفة تباهت باستقلاليتها. مما أدى لتبني كلا منها لعملتها وأوزانها ومقاييسها الخاصة الخ. وأوجد هذا اختلافات صغيرة في نظام الأرقام بين الولايات المختلفة لأن نظام الأرقام قديما كان يستخدم بصورة كبيرة في المعاملات التجارية. ومع ذلك فإننا لن نفحص بالتفصيل في هذه المقالة الاختلافات الصغيرة في نظام الأرقام في هذه الولايات، بل سنلقي نظرة على هيكله العام. من البداية علينا توضيح أن الإغريق كان لديهم أنظمة مختلفة للأعداد الأصلية (cardinal) والترتيبية (ordinal)، لذا علينا توضيح ما نعنيه بأنظمة الأرقام اليونانية. أيضا سنبحث سريعا أنظمة أرقام اقترحها بعض علماء الرياضيات اليونانيون ولكنها لم تلق قبولا واسعا.

أول نظام أرقام يوناني سنبحثه هو نظامهم الأكروفوني المستخدم في الألفية الأولى قبل الميلاد. والأكروفوني "Acrophonic" (من الكلمتين اليونانيتين ἄκρος أكروس بمعني بداية و  φωνή فون بمعني صوت) يعني أن رمز الرقم يأتي من الحرف الأول من اسمه، لذا فالرمز أتى من الكلمة المختصرة المعبرة عن الرقم. فيما يلي رموز الأرقام 5، 10، 100، 1000، 10000.

الأرقام الأكروفونية 5، 10، 100، 1000، 10000.

الأرقام الأكروفونية 5، 10، 100، 1000، 10000.

لقد أغفلنا رمز "الواحد" ، وهو ببساطة "|"، وبشكل واضح لم يأت من الحرف الأول للرقم. بالنسبة لـ 5، 10، 100، 1000، 10000 سيدرك القارئ أن رمز 5 عبارة عن لغز، فطبقا لهذا النظام كان يجب استخدام P وهو الحرف الأول من كلمة Pente (وتعني خمسة باليونانية). ببساطة يرجع السبب لتغير الأبجدية اليونانية وبقيت الحروف الأولى لكلمات الأرقام على سابق عهدها. ربما لم يكن يُعتقد أن رموز الأرقام أتت من الحروف، لذا بقيت على حالها. فالشكل الأصلي لـ حرف باي اليوناني π  كان Γ (مثل حرف الجاما ولكن في نهاية الخط الأفقي انحناءة للأسفل) لذا Pente كانت تكتب كـ Gente (ملاحظة هنا أعتقد أنه اختلط الأمر على مؤلف المقالة، فحرف الباي ظل على نطقه القديم لكن تغير شكله فقط).

اعتمد النظام مبدأ الإضافة كالأرقام الرومانية. ببساطة 8 هي VIII، أي رمز الخمسة متبوعًا بثلاثة رموز للواحد. هذه الأرقام اليونانية من  1 الى 10 بالنظام الأكروفوني.

الأرقام اليونانية الأكروفونية من 1 الى 10.

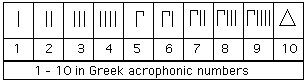الأرقام اليونانية الأكروفونية من 1 الى 10.

لو استخدمنا النظام العشري مع مبدأ الاضافة بدون رموز وسط، فسنحتاج للعديد من الحروف لتمثيل أعداد معينة. فعدد كـ 9999 سيتطلب 36 رمزًا في نظام كهذا وهو أمر مرهق جدًا. ذكرنا أن الأرقام الصوتية اليونانية احتوت على رمز خاص ل 5، وهذا طبيعي لأنه سيقلل الأحرف المطلوبة لتمثيل الأعداد ونشأ من العد على الأصابع (10 أصابع، 5 في كل يد). والمدهش أن النظام احتوى على رموز وسيطة لـ 50 و 500 و 5000 و 50000 لكنها لم تكن حروف جديدة، بل مركبة من 5 ورموز لـ 10 ، 100 ، 1000 ، 10000 على التوالي. هنا ترى تركيب لتلك الأعداد.

تركيب أرقام أكروفونية.

تركيب أرقام أكروفونية.

لاحظ لأنه نظام غير موضعي، لذا ليس هناك حاجة للصفر للتعبير عن خلو الموضع. فرمز H يعبر عن العدد  100 ولا حاجة لاستخدام أرقام بها عشرات أو وحدات.

ليست هذه الطريقة الوحيدة لإنشاء هذه الرموز المركبة. ذكرنا بالفعل أن ولايات عدة استخدمت أنظمة أرقام متنوعة، وبرغم أننا لن نبحثها بالتفصيل، وكن على الأقل سنشير لها بعرض بعض صور العدد 50 التي عُثِرَ عليها. معظمها أقدم من صور الأرقام الرئيسية والتي تعتبر أكثر نمطية في الفترة من 1500 ق. م لـ 1000 ق. م.

صور مختلفة للعدد 50 من عدة ولايات يونانية.

صور مختلفة للعدد 50 من عدة ولايات يونانية.

جدير بالذكر أن نظام الأرقام هذا لم يكن مكونًا من أرقام مجردة بالطريقة التي ننظر بها الآن للأرقام. الآن الرقم 2 يستخدم للدلالة على أي مجموعة تحتوي على عنصرين، ويُنظر للرقم 2 على أنه خاصية مجردة تشترك فيها كل هذه المجموعات الثنائية العناصر. نعرف أن فكرة الإغريق القدماء عن الأرقام كانت مختلفة لحد ما، حيث يختلف شكل الرقم بحسب ما يدل عليه. كان عد الأموال هو الاستخدام الشائع لنظام الأرقام هذا. وكانت الدراخما هي الوحدة الأساسية للمال مع وحدة أكبر هي الطالنط والتي تساوي 6000 دراخما. قُسِمتْ الدراخما لوحدات أصغر، وهي الأوبول والذي كان 1/6 الدراخما والخالكوس (χαλκός بمعنى نحاس)  وكان 1/8 من الأوبول. استخدم أيضا نصف وربع الأوبول. لاحظ أن نظام العملة هذا لم يكن عشريا  برغم احتوائه على 10 كأساس و 5 كأساس ثانوي.

أُشير لوحدات العملة المختلفة بتعديل تدوين الوحدات في العدد.

دُوِنَت 5678 دراخما بهذه الطريقة:

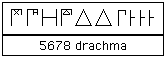5678 دراخما

شكل الوحدات سيشير للدراخما.

ودُوِنَت 3807 طالنط على النحو التالي:

3807 طالنط

وترى الآن الوحدات ممثلة بـ T (T لكلمة طالنط τᾰ́λαντον). ولتدوين مبلغ من المال فيه دراخما وأبولات سيكون على النحو التالي:

3807 دراخما و3 أبولات:

3807 دراخما و3 أبولات

استخدم هذا النظام الأكروفوني لما هو أكثر من المال. فاُستخدِم نظام مشابه جدًا للتعامل مع الأوزان والمقاييس وهو أمر لا يثير الدهشة لأن قيمة المال تطورت بالتأكيد من نظام للأوزان. ويؤكد هذا حقيقة أن الدراخما كانت أيضًا اسما لوحدة الوزن.

لنفحص الآن نظام الأرقام اليوناني القديم الثاني، وهو الأرقام الأبجدية، أو كما يسمى أحيانًا نظام "المتعلمين". كما يقترح الاسم، فإن الأرقام تستند لقيم معطاة للحروف الأبجدية. وجدير بالذكر أن الإغريق كانوا من أوائل من استخدموا نظام أبجدي للكتابة. لم يخترعوا هذا الشكل من الكتابة الأبجدية، لأن الفينيقيين سبقوهم إليه. فأخذ اليونانيون عن النظام الفينيقي الأبجدية اليونانية المستخدمة في الكتابة وكانت قريبة جدًا منها. لن نبحث أشكال الحروف اليونانية نفسها، لكن بكل تأكيد ساهم هذا الشكل من الكتابة في تقدم المعرفة. وهو الطريقة الأساسية للتواصل في معظم البلاد حاليا، رغم أن بعض الناس تفضل استخدام طرق أخرى للكتابة.

هناك 24 حرفًا في الأبجدية اليونانية الكلاسيكية و3 أحرف قديمة بَطُلَ استخدامها (ديجاما ϛ، سان Ϻ، وكوبا Ϙ). هذه هي الأحرف الـ 27 

الحروف اليونانية القديمة

عرضنا هنا صور الحروف الكبيرة والصغيرة الـ 24. عدا الحروف ديجاما وكوبا وسان التي بَطُلَ استخدامها. وبرغم أننا لم نعرض رموزهم في الجدول أعلاه ولكن رموزهم معروضة في جداول الأرقام أدناه. اتخذت التسعة حروف الأولى منها كرموز للأرقام 1، 2، ...، 9.

الأرقام الأبجدية 1-9.

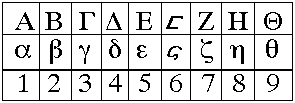الأرقام الأبجدية 1-9

لاحظ أن الرقم 6 مُمثل برمز خاص بالحرف القديم ديجاما .

أتخذت الحروف التسعة التالية كرموز لـ 10، 20، ...، 90.

الأرقام الأبجدية 10-90.

الأرقام الأبجدية 10-90.

لاحظ أن الرقم 90 ممثل برمز الحرف القديم كوبا.

أتخذت الحروف التسعة المتبقية كرموز لـ 100، 200، ...، 900.

الأرقام الأبجدية 100-900.

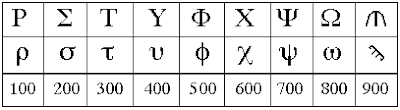الأرقام الأبجدية 100-900.

لاحظ أن 900 ممثل برمز الحرف القديم سان.

أحيانا عند استخدام هذه الحروف لتمثيل الأرقام، يوضع شريط فوق الرمز لتمييزه عن الحرف المقابل.

يتم تكوين الأعداد عن طريق مبدأ الإضافة. كمثال نكتب 11، 12، ...، 19:

الأرقام الأبجدية 11-19.

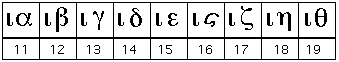الأرقام الأبجدية 11-19

ولأعداد أكبر نستخدم نفس الطريقة. كمثال هنا 269.

العدد الأبجدي 269.

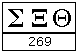العدد الأبجدي 269

هذا النظام مدمج ولكن بدون تعديلات يعيبه بشكل كبير عدم قدرته على التعبير أعداد أكبر من 999. لذا وُضِعَتْ رموز مركبة للتغلب على هذا القصور. تُمَثَلْ الأعداد بين 1000 و 9000 عن طريق إضافة حرف إيوتا سفلي أو علوي للأرقام من 1 إلى 9.

شكل أول للأعداد 1000، ...، 9000.

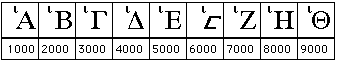شكل أول للأعداد 1000، ...، 9000

شكل آخر للأعداد من 1000، ...، 9000.

شكل آخر للأعداد من 1000، ...، 9000

كيف مَثَلَ اليونانيون الأعداد الأكبر من 9999؟ حسنًا، لقد أسسوا لأعدادهم الأكبر من ذلك على مفهوم "العدد الذي لا يحصى" (μυριάς) والذي كان 10000. الرمز M وأعلاه رقم أبجدي صغير حتى 9999 يعني أن العدد الممثل بالرقم الأبجدي الصغير مضروب في 10000. لذا فإن وضع β فوق M تعني أن العدد 20000  (2 ممثلة ب β مضروبة في 10000):

العدد 20000.

العدد 20000

بالمثل العدد الأبجدي ρκγ (يمثل 123) فوق M يمثل 1230000:

العدد 1230000.

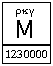العدد 1230000

بالطبع، وضع عدد كبير فوق M كان أمرًا مرهقًا لحد ما، وكثيرا ما وُضِعَ العدد الأبجدي الصغير أمام M وليس فوقه. كمثال من أرسطرخس الساموسي:

كتب أرسطرخس العدد 71755875 كذا:

كتابة أرسطرخس للعدد 71755875

لمعظم الاستخدامات يمكن أن يمثل نظام الأرقام هذا جميع الأرقام في الحياة اليومية العادية. بالواقع، من النادر وجود أعداد كبيرة مثل 71755875. من جانب آخر، فهم علماء الرياضيات الحاجة لتوسيع نظام الأرقام ولنبحث اقتراحين لهذا الغرض، الأول لأبولونيوس ثم بعده بفترة وجيزة آخر لأرخميدس ( برغم أنه تاريخيًا قدم أرخميدس اقتراحه قبل أبولونيوس بحوالي 50 عامًا).

على رغم أنه اقتراح أبولونيوس لم يصلنا منه مباشرة، إلا أنه وصلنا مما كتبه ببس الرومي عنه. النظام المشروح أعلاه استخدم الضرب بـ "العدد الذي لا يحصى" (μυριάς). كانت فكرة أبولونيوس لتوسيع النظام لأعداد أكبر هي استخدام مضاعفات "العدد الذي لا يحصى" (μυριάς). فوضع الرقم الأبجدي α فوق M يُعطي 10000، M فوقها β يُعطي M2، أي 100000000، وهكذا. والرقم المراد ضربه في 10000، 10000000، إلخ ، يُكْتَبْ بعد الرمز M والكلمة χαι (ولعلها και بمعنى واو الإضافة) تكتب بين أجزاء العدد، وهي كلمة تُفَسَر على أنها "زائد". كمثال هنا طريقة أبولونيوس لكتابة  587571750269.

تمثيل أبولونيوس للعدد 587571750269.

تمثيل أبولونيوس للعدد 587571750269

صمم أرخميدس نظامًا مشابهًا ولكن بدلاً من استخدام $10000=10^4$  كعدد أساسي يُضاعف لقوى مختلفة قام باستخدام 100000000=108، مضاعفًا لقوى مختلفة. تكونت أول مجموعة ثمانية لأرخميدس من الأعداد حتى 108 وكانت المجموعة الثمانية التالية من الأرقام من 108 حتى 1016. أرخميدس وباستخدام هذا النظام، حَسَبَ عدد حبيبات الرمل التي يمكن ملئ الكون بها وتوصل إلى أنها من رتبة المجموعة الثمانية الثامنة ، أي برتبة 1064.

المصادر:

1. G Ifrah, A universal history of numbers : From prehistory to the invention of the computer (London, 1998).

📗 طالع أيضاً:

• طالع ترجمة لمقالة نظام الأرقام العربية.
• طالع ترجمة لمقالة الأرقام الهندية.
• طالع ترجمة لمقالة تاريخ الصفر.
• طالع ترجمة لمقالة الأرقام المصرية.
• طالع ترجمة لمقالة رياضيات المايا.
• طالع ترجمة لمقالة الأرقام البابلية.