كان لدى المصريون نظام كتابة معتمد على الهيروغليفية مذ حوالي 3000 ق. م. الهيروغليفية هي صور صغيرة تمثل الكلمات. من السهل أن نعرف لم خصصوا صورة طائر صغير للدلالة على كلمة طائر، لكن من الواضح قصور هذا النظام والحاجة لتطويره ليمثل كلمات أخرى. حل المصريون القدماء هذه المشكلة عن طريق استخدام الصوت المنطوق للكلمات. كمثال لتوضيح الفكرة بمثال من اللغة الإنجليزية (I hear a barking dog) "أنا أسمع كلب ينبح" يمكن تمثيلها صورياً بـ "🐶👑🌴👂👀"
👀 (صوت الكلمة يعبر عن كلمة I بمعنى أنا)، 👂 (صوت الكلمة يعبر عن كلمة hear بمعنى يسمع)، 🌴(صوت الكلمة يعبر عن كلمة bark بمعنى ينبح)، 👑(صوت الكلمة يعبر عن كلمة king تضاف للكلمة السابقة عليها لتعطي الصوت الكامل لكلمة barking)، 🐶(بمعنى كلب).
وبالطبع نفس الرموز يمكن أن تُستخدم بشكل مختلف في سياقات أخرى، لذا صورة العين ممكن أن تعني يرى وصورة الأذن ممكن أن تعني يسمع.
كان للمصريين نظام أرقام عشري برموز هيروغليفية تمثل الأرقام. ونعني بهذا أنه كان هناك رمز هيروغليفي يمثل واحد وعشرة ومائة وألف وعشرة آلاف ومائة ألف ومليون.
هذه الرموز الهيروغليفية تمثل الأرقام التي ذكرناها
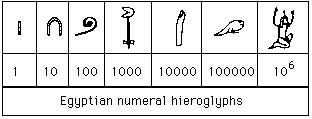 |
| أرقام هيروغليفية مصرية |
 |
| رقم 276 في نظام الأرقام الهيروغليفي المصري |
هذا مثال آخر
 |
| رقم 4622 في نظام الأرقام الهيروغليفي المصري |
لاحظ هنا أن المثالين السابقين لكلا الرقمين 276 و 4622 كانوا محفورين على صخرة من الكرنك، ترجع لحوالي 1500 ق. م، ومعروضة الآن في متحف اللوفر بباريس.
يمكن بسهولة توضيح سهولة إضافة الأرقام الهيروغليفية. نجمع فقط الرموز الفردية، ثم لكل عشر نسخ من نفس الرمز نضع محله رمز يمثل قيمة هذه الرموز مجتمعة. كانت الكسور عند قدماء المصريين مقتصرة فقط على كسر الواحد (مع استثناء الكسر المستخدم بكثرة ⅔ والأقل استخداما ¾ ). كسر الواحد يأتي على الشكل التالي n⅟ حيث n عدد صحيح، وكانت هذه الكسور تُمثل في الأرقام الهيروغليفية عن طريق وضع رمز يمثل "الفم" 𓂋 ومعناه "الجزء" فوق الرقم، هذه بعض الأمثلة:

|

|

|
لاحظ في حالة كون الرقم في المقام كبيرا، فإن رمز "الجزء" يوضع فقط على الجزء الأول من الرقم، كما هو الحال في المثال المعروض أعلاه في الرقم 249⅟ [الجزء الأول كما في الصورة حيث يُقرأ الرقم من اليمين لليسار.]
علينا أن نذكر أن الكتابة الهيروغليفية لم تستمر بنمط واحد خلال الألفي سنة أو أكثر من الحضارة المصرية القديمة. هذه الحضارة تُقسم غالباً لثلاث فترات مختلفة:
المملكة القديمة - حوالي 2700 ق. م. حتى 2200 ق. م.
المملكة الوسطى - حوالي 2100 ق. م. حتى 1700 ق. م.
المملكة الحديثة - حوالي 1600 ق. م. حتى 1000 ق. م.
الأرقام الهيروغليفية اختلفت لحد ما تبعا للثلاث فترات المذكورة، لكن ظل نمط كتابتها متشابها لحد كبير.
استخدم المصريون نظام أرقام آخر بعد اختراع الكتابة على ورق البردي وفيه اُستعملت الأرقام الهيراطيقية. هذه الأرقام الهيراطيقية سهلت كتابة الأرقام في شكل أقل حجما ولكن تطلب هذا تَذكُر عدد كبير منها. كان هنا رموز منفصلة ل
1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 20, 30, 40, 50, 60, 70, 80, 90,
100, 200, 300, 400, 500, 600, 700, 800, 900,
1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000
وهذه أشكال الأرقام الهيراطيقية
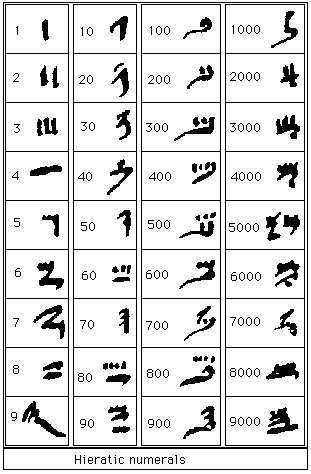 |
| الأرقام الهيراطيقية |
فباستخدام هذا النظام ستُكتب الأرقام برموز أقل. فالرقم 9999 يُكتب بأربعة رموز هيراطيقية فقط، بدلاً من 36 رمز هيروغليفي. فارق آخر كبير بين نظام أرقامنا الحالي ونظام الأرقام الهيراطيقي كان في أن نظام الأرقام الهيراطيقي لم يكن نظاماً موضعياً، ويمكن وضع رموز الأرقام بأي ترتيب.
هنا مثلا طريقة كتب بها المصريون الرقم 2765 بالأرقام الهيراطيقية
وهنا طريقة أخرى لكتابة الرقم 2765 بالأرقام الهيراطيقية بترتيب معكوس
تغيرت الرموز الهيراطيقية على مر الزمن كما حدث للهيروغليفية، لكن تعرضت لتغيير أكبر خلال ست فترات مختلفة. في البداية كانت الرموز الهيراطيقية قريبة جدا لما يُماثلها في الهيروغليفية ولكن اختلف شكلها بمرور الزمن. الأمثلة التي عرضناها بالأعلى للرموز الهيراطيقية تعود لحوالي 1800 ق. م. اُستخدم النظامان الهيروغليفي والهيراطيقي بالتوازي لما يقرب من 2000 عام مع استخدام الرموز الهيراطيقية في الكتابة على البردي، كما في برديتي ريند وموسكو، بينما اُستخدمت الرموز الهيروغليفية في النقش على الحجر.
المصادر:
- R Calinger, A conceptual history of mathematics (Upper Straddle River, N. J., 1999).
- G Ifrah, A universal history of numbers : From prehistory to the invention of the computer (London, 1998).
- G G Joseph, The crest of the peacock (London, 1991).
📗 طالع أيضاً:
- ترجمة لمقالة نظام الأرقام العربية.
- ترجمة لمقالة الأرقام الهندية.
- ترجمة لمقالة تاريخ الصفر.
- ترجمة لمقالة رياضيات المايا.
- ترجمة لمقالة الأرقام البابلية.
- ترجمة لمقالة أنظمة الأرقام اليونانية.


جميل جدا
ردحذفوجهد مشكور
شكراً جزيلاً
حذفمعلومات قيمة مصاغة بعناية ومجهود بحثي رائع
ردحذفبارك الله فيك ونفع بك
شكراً جزيلاً
حذف